Статус: Офлайн
Реєстрація: 05.02.2009
Повідом.: 30271

Реєстрація: 05.02.2009
Повідом.: 30271

Подскажите решение топологической задачи.
Задача следующая:
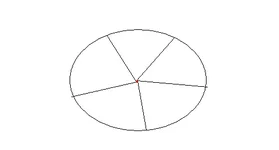
1. Пять территорий на плоскости.
2. У всех пяти есть общие границы.
Есть ли решение этой задачи, интересует как математическое, так и наглядное, иллюстративное/наглядное решение.
Буду рад любой помощи.
Задача следующая:
1. Пять территорий на плоскости.
2. У всех пяти есть общие границы.
Есть ли решение этой задачи, интересует как математическое, так и наглядное, иллюстративное/наглядное решение.
Буду рад любой помощи.





 .
.