Там нет примера, который можно использовать практически....
.... А что это за экселевский файл?
Экселевский файл
мой. Написан
за 10 минут на основе примера расчёта по ссылке, который Вы в упор не видите. Та самая искомая
практическая реализация очень внятного и толкового объяснения способа решения задачи.
При желании легко добавить в данные столбик COS фи,
отдельно для каждой фазы, и считать при
любом характере нагрузки.
Объяснение есть. По ходу, Вы его не заметили, не вникли, проигнорировали.
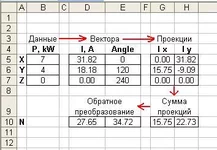
выразите вектора токов через их проекции на оси X и Y, сложите проекции всех фазных токов, как результат - получите проекции тока нейтрали. Потом обратное преобразование координат и - voilà - имеем вектор тока в нейтрали.
Это путь, как графическое решение задачи превратить в аналитическое.
Именно он реализован в таблице. Стрелками и словами, для наглядности, показано что из чего считается.
дескать мы такие умные, знаем, что такое векторное суммирование, а вы ваньки не знаете.
Снова повторюсь -
все формулы и методы, использованные при расчёте взяты из
школьного курса тригонометрии. Если Вы, не по наслышке, знакомы с учебником Каплана, то преобразовать полярные координаты в прямоугольные и наоборот у Вас не должно вызывать не малейших затруднений. А, по ходу, вызывает. С этого мне надо было начинать объяснение? Или с классического "
В нача́ле бы́ло Сло́во"?
Но так не поступают, когда хотят что-то объяснить другому человеку. Так поступают лишь когда хотят покрасоваться собой любимым.
Простите.
Я Вам дал ссылку на методику, по которой решается задача. Лично для меня, там содержится
исчерпывающая информация
с примером расчёта.
Потом словами, по шагам объяснил, как решить её аналитически и, наконец,
дал скриншот таблицы, в которой реализован и
прокомментирован описанный алгоритм и
решена задача при поставленных Вами исходных.
В чём я покрасовался? В том, что до сих пор помню и пользуюсь знаниями полученными в средней школе? Так, по-моему, это нормально. В смысле помнить и пользоваться.
Можете прислать ссылку на источник, либо сам файл?
А самостоятельно, как Вы любите, разобраться не хотите? Даже в этой теме уже более чем достаточно информации по вопросу.
Не то что бы мне было жалко задаром отдать нажитое непосильным трудом, но тяжело верится, что человек, с такой любовью и уважением говорящий об учебнике высшей математики, не способен решить школьную задачу.
В помощь - любимая
⚠ Тільки зареєстровані користувачі бачать весь контент та не бачать рекламу.
. Там есть формулы преобразования длины и угла вектора в проекции на X - Y и обратно. Ссылку на сложение столбиком давать не буду. Верю в Ваши силы!
Удачи!
На уровне школьной тригонометрии. 
Кнопки вам за это на стул не подкладывали? 
