Кто посчитает?

[doktor_7878]

Кто посчитает?

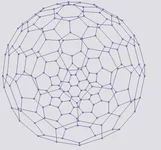
Как покрыть сферу равными шестигранниками.
Радиус сферы около 3м
Площадь шестигранника около 1м.кв.
Все углы и ребра должны быть одинаковые, сфера должна быть визуально, а математически можно не правильную.
Сколько будет стоить?
Предложения в личку, спасибо.

 

[Андрей 1980]

Расчитал бы сам, но чертежные программы еще не переустановил. Обратись в раздел работа там много чертежников и расчетчиков.

 

[BOBAHH]

Как покрыть сферу равными шестигранниками.
Радиус сферы около 3м
Площадь шестигранника около 1м.кв.
Все углы и ребра должны быть одинаковые, сфера должна быть визуально, а математически можно не правильную.
Сколько будет стоить?
Предложения в личку, спасибо.

Вы просите сделать не возможное. Судя по вашему вопросу, для того чтобы вам объяснить это потребуется преподать краткий курс аналитической геометрии.
Наберите в Вики "Платоновы тела" может поймёте.

 

[doktor_7878]

Не не не, можно как мяч, шести и пятигранники.
Вот по образцу Посилання видалено
Нужен расчет длинны ребер(должны быть одинаковые) и углов, и картинку как это будет выглядеть.

 

[BOBAHH]

Не не не, можно как мяч, шести и пятигранники.
Вот по образцу Посилання видалено
Нужен расчет длинны ребер(должны быть одинаковые) и углов, и картинку как это будет выглядеть.

Ты бы так и говорил.
Посилання видалено
Ну а посчитать там - дело 10 минут.

 

[doktor_7878]

Ты бы так и говорил.
Посилання видалено
Ну а посчитать там - дело 10 минут.

Так посчитайте, скажите сколько денег?

 

[Razgon]

Не не не, можно как мяч, шести и пятигранники.
Вот по образцу Посилання видалено
Нужен расчет длинны ребер(должны быть одинаковые) и углов, и картинку как это будет выглядеть.

Коких углов? в равносторонних пяти- и шестиугольниках углы одинаковые и неизбежно предопределены. Сумма углов многоугольника равна (n-2)*180 градусов, где n - число граней многоугольника. Каждый угол будет (n-2)*180/n.

Длины ребер. Площадь равностороннего 6-угольника - S=3*sqrt(3)*a^2/2, кажется, где а - сторона. Площадь сферы S1=4*pi*r^2, где r - радиус сферы. Нам нужно, чтобы площадь некоей поверхности, состоящей из многоугольников со стороной а, была как можно более близка к площади этой сферы.
n*S < S1 < (n+1)*S
Отсюдова и найдем n.

 

[unza]

doktor_7878, если попроще описать изложенное Razgon, то вы задаетесь площадью сферы и колчеством углов в многоугольнике. Из нее получаете радиус сферы, и длину стороны многоугольника .
И как везде есть нюанс - для многоугольников, расположенных на сфере выражение "Сумма углов многоугольника равна (n-2)*180" ошибочно ...

 

[Razgon]

И как везде есть нюанс - для многоугольников, расположенных на сфере выражение "Сумма углов многоугольника равна (n-2)*180" ошибочно ...

Нет, конечно, в данном случае В данном случае стороны многоугольников не лежат на сфере, а хорды.
Нюансов действительно масса. И то, что я написал, на самом деле неправильно, но работать как-то будет, тем более ТСу не надо идеальной кругляшки

 

[doktor_7878]

Нет, конечно, в данном случае В данном случае стороны многоугольников не лежат на сфере, а хорды.
Нюансов действительно масса. И то, что я написал, на самом деле неправильно, но работать как-то будет, тем более ТСу не надо идеальной кругляшки

Кругляшки не надо, но все должно сойтись. Есть программы Компас(по-моему) я пытался потроить отсечением плоскотями, не получилось. Толи погрешности дает программы, не знаю.

,

 

[Achenar]

Сегодня вечерком или выдам список координат, или признаю свою ******ь

В общем, не решается. По одной простой причине - место стыка трех шестиугольников - это ********, стоящая на сфере, причем углы вокруг вершины равны по 120 градусов (угол шестиугольника). Но тогда вершина стоит внутри угла в 360 градусов и "не может оторваться" от плоскости, касательной к сфере, то есть все три шестиугольника лежат в одной плоскости, а это не есть хорошо, надо же их "изломать", чтобы они начали охватывать сферу.

В проекте "Эден" сделана попытка, но там и пятиугольники присутствуют, и шестиугольники кривые. В данной постановке, к сожалению, задачу решить невозможно.

 

[doktor_7878]

Сегодня вечерком или выдам список координат, или признаю свою ******ь

В общем, не решается. По одной простой причине - место стыка трех шестиугольников - это ********, стоящая на сфере, причем углы вокруг вершины равны по 120 градусов (угол шестиугольника). Но тогда вершина стоит внутри угла в 360 градусов и "не может оторваться" от плоскости, касательной к сфере, то есть все три шестиугольника лежат в одной плоскости, а это не есть хорошо, надо же их "изломать", чтобы они начали охватывать сферу.

В проекте "Эден" сделана попытка, но там и пятиугольники присутствуют, и шестиугольники кривые. В данной постановке, к сожалению, задачу решить невозможно.

Так я давно написал, конечно и шести ипятиугольники. И у меня тоже есль прдположения, что они будут кривые.
Вчера клип видел какой-то нашей спивачки, так она снималась на фоне такой большой сферы, но она из маленьких треугольников.
Что бы было понятней это должна бать реальныя конструкция. С минимальными затратами на призводство и простой в сборке. Т.е. хотелось бы иметь одинаковые трубки и тройнички для их соединения в конструкцию-сферу.
Короче если есть решение в треулодьниках оно тоже подойдет.

 

[Achenar]

В общем, половинку сферы пока прикинул, повращайте, посмотрите. Пустые места заделываются пятиугольниками (первый ярус "прорех"), затем можно доклепать треугольниками. Все сделал по максимуму однотипным. "Смета" для полусферы:

1. 12 шестиугольников 0.89м (да, большие, но иначе надо делать 0.5м и их будет 24 - фишка в том, чтобы в "поясе" сферы было именно 12 шестиугольников, тогда наверх пойдет по 6 шестиугольников и увенчается одним в зените).

2. Еще 6 шестиугольников 0.89м - второй ярус.

3. 6 пятиугольников 0.89х4 + не считал - "прорехи" второго яруса.

4. 6 больших треугольников над пятиугольниками.

5. 12 маленьких по сторонам от больших.

7. 6 шестиугольников в последнем перед "зенитом" ярусе, 0.8м.

6. Одинаковые небольшие треугольники возле последнего шестиугольника (0.85м) в зените.

Если размер шестиугольника 0.8+ неприемлем - ну, тогда проблем становится больше

Или вот с трехлистником сверху, тогда меньше проблем с треугольниками. И шестиугольники со стороной 0.89, 0.6, 0.52 и 0.5м.

 

[doktor_7878]

)))Да, примерно такое получалось у меня. Тут размеры не так важны, как красивая форма.

 

[Achenar]

В общем, умудрился все сделать без пятиугольников и треугольников. Что означает, что собрать можно и на тройниках (скажем, если в треугольниках решать, то надо делать не тройники, в одной точке сходится 6 ребер).

Могу выдать координаты тройников, направления стержней и длины стержней.

Тройников получилось 192, стержней - 294.

Материальная сторона вопроса присутствует ?

А, нет, есть штук шесть пятиугольников. Но все равно в тройниках собирается.

288 стержней, программа сглючила и шесть стержней в одну и ту же точку поместила. На результат это не влияет. Группы стержней одной длины по 12, 24 и 48 штук, всего 12 различных видов стержней (или 13, если 2мм что-то решают). Все длины внутри одной группы одинаковые с точностью до микрона.

 

[Achenar]

Минимальный вариант на 90 стержней по 1.22 метра.